实用且最优的角距离局部敏感哈希算法
论文主要研究 Cross-polytope LSH 算法,包括理论分析(Optimal)和性能改进(Practical),我这里只关心后者。
Cross-polytope LSH
Cross-polytope LSH 的距离度量是角距离(angular distance),等效于归一化到单位球面上之后的欧拉距离。
算法定义为用 N(0, 1) 随机初始化一个矩阵 A,计算 y = Ax / ||Ax||(也就是随机旋转),之后取最近的一个正或负的单位向量为其哈希值(也就是 argmax[Ax, -Ax])。
对 Cross-polytope LSH 的三个小改进
意义都不大:
- 伪随机旋转:$A = HD_3HD_2HD_1$,其中 H 为 Hadamard 矩阵($\pm 1$ 构成的正交方阵),三个 D 都是对角元素为随机 $\pm 1$ 的对角矩阵
- 空间:H 是固定的,不算空间。D 是对角的。所以由 O($d^2$) 降为了 O(d)
- 时间:用快速 Hadamard 变换(视频编码领域的经典算法,我不懂)可以由 O($d^2$) 降到 O($d \log d$)
- 作者没有证明这种方法与原方法的等效性,只指出两个 H 不够,三个 H 可以
- 特征哈希:如果是稀疏向量,先做一个随机的哈希(各列只有一个 $\pm 1$)使维度降下来
- 部分 Cross-polytope LSH:最后只从部分单位向量中取最近,相当于把 [Ax, -Ax] 的部分维度给去掉了
Multiprobe LSH
想法:
- 对 LSH 来说,如果 p, q 相近,那 h(p) 与 h(q) 即使不在同一个桶中,也应该在相近的桶中
- 对 Cross-polytope LSH 来说,h(p) 的分布按概率大小排列应该与 sort[Aq, -Aq] 相同,即最可能与 argmax[Aq, -Aq] 碰撞,其次可能与 [Aq, -Aq](记为 z)中第二大的位置碰撞,...
以上是定性的分析,作者又定量地计算出,在 A 中元素满足高斯分布的前提下近似地有, $$P{h(p) = i} \propto \exp{-|\max z - z_i|^2}$$
通常 LSH 都是要经过多轮哈希的,之前的方法是每一轮哈希只看最大值位置是否碰撞。
但有了前面的定量结论就可以把多轮旋转结果合一起按概率排序,看概率最高的几个位置是否碰撞,就能更好地利用旋转运算的结果。如图:
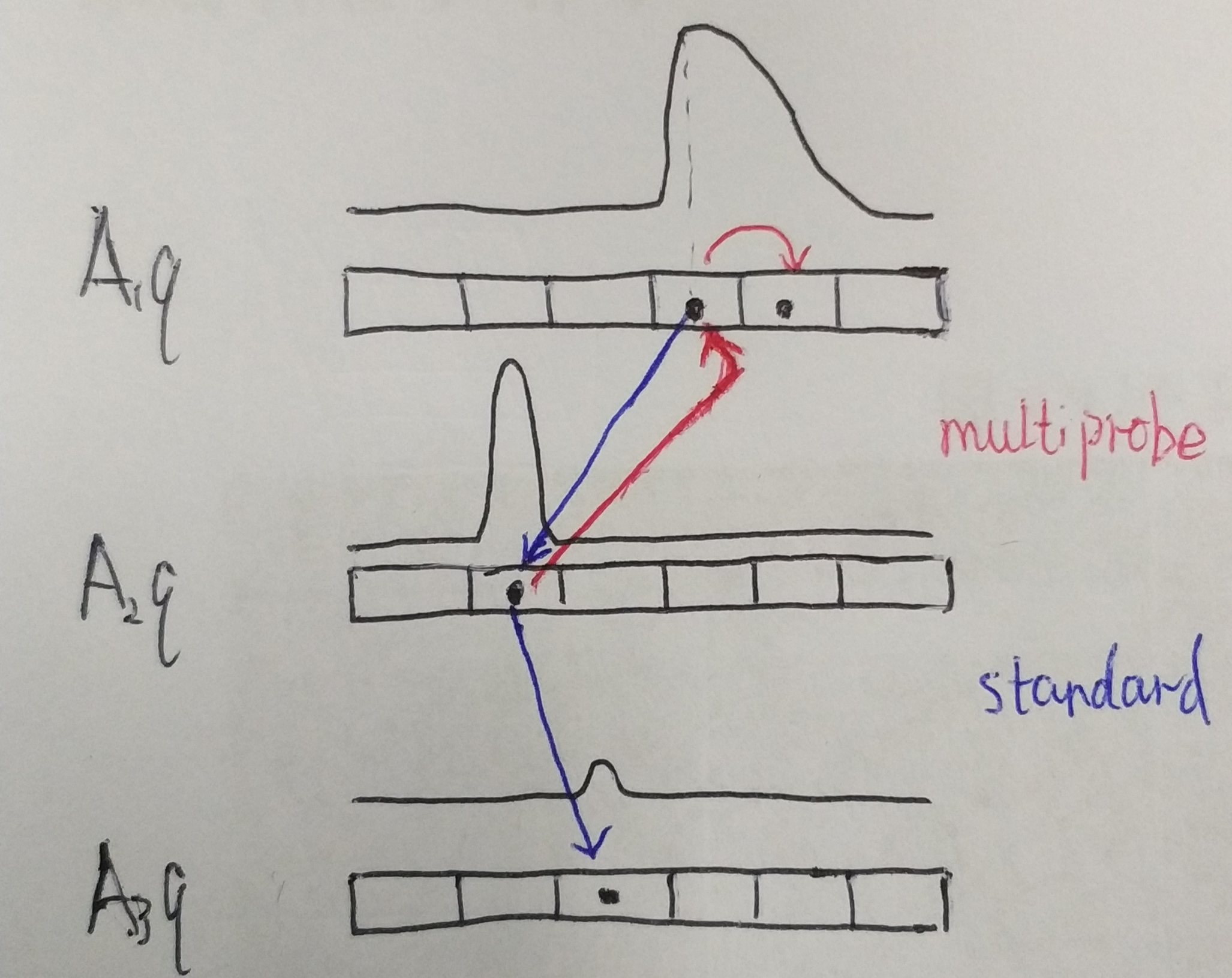
上面方法之所以可行,是因为有时候 q 的旋转结果更接近“边界”,p 的哈希结果落到相邻区域的概率也不低,落到 q 的区域的概率相应地就不高了。
补充:因为原文说得不清楚,只说求出概率后用与《高维相似搜索中的多探头 LSH 索引》中的方法构造出序列。我猜着画了前面的图,但看完引用的文章后发现图画得不对,不改了。
Page Not Found
Try to search through the entire repo.