使用混合模型的卷积神经网络做图与流形的几何深度学习
模型
$$D_j(x)f = \sum\limits_{y \in N(x)} w_j(u(x, y))f(y), j=1, \cdots, J$$
$$(f * g)(x) = \sum\limits_{j=1}^{J} g_jD_j(x)f$$
- 其中 u(x, y) 是相对位置/伪坐标,这个设定使得方法适用于流形
- w 将其映射到一个权重上,这样可以在不同位置共享参数
便于理解,可以认为是定义了如下形式的卷积运算: $$f * g = g (Wu) f$$
不少已有模型都可看作这个框架的特例

u(x, y) in CNN:
| (-1, -1) | (0, -1) | (1, -1) |
|---|---|---|
| (-1, 0) | x | (1, 0) |
| (-1, 1) | (0, 1) | (1, 1) |
GCN: $$f * g = \theta (I_n + D^{-\frac{1}{2}}AD^{-\frac{1}{2}})f$$
DCNN: $$H^{(k)} = f(W^{(k)} \odot (D^{-1}A)^k X$$
论文中使用的可学习的权重函数: a Gauusian Mixture Model (GMM) $$w_j(u) = \exp (-\frac{1}{2} (u-\mu_j)^T \Sigma_j^{-1} (u - mu_j))$$ 其中 $\Sigma_j$ 是 d x d 的协方差矩阵且限制为对角的(也就是假设各分量独立),$\mu_j$ 是 d 维的均值向量。这样共 2dJ 个参数需要学习。
实验
图片分类
一是使用 LeNet,二是将图片转为图使用 CheNet 和 MoNet

LeNet 最好,MoNet 稍差。
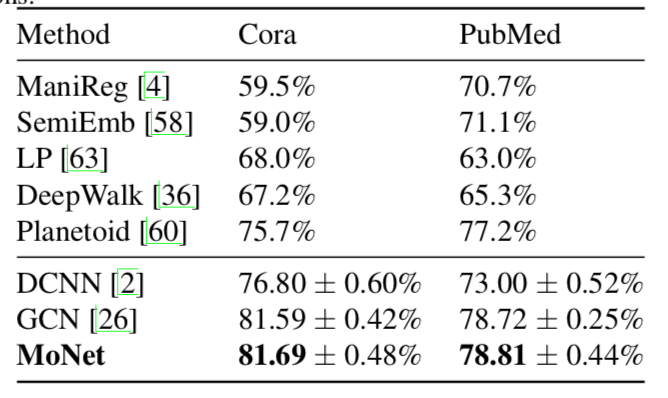
图链接预测
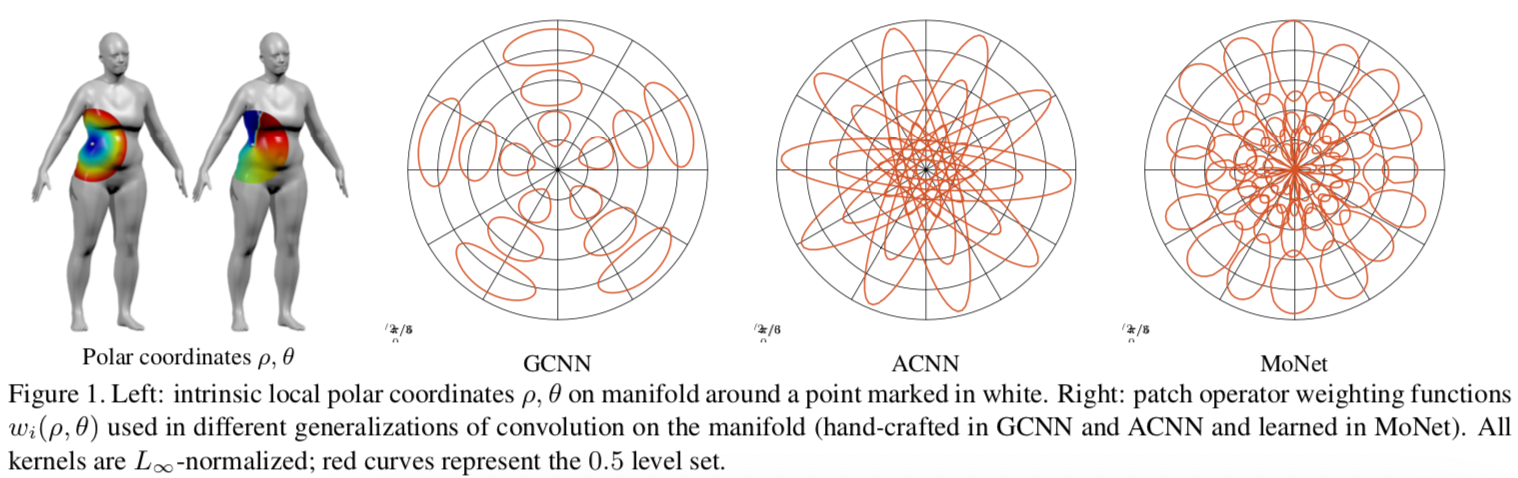
流形上的学习
Page Not Found
Try to search through the entire repo.