图变分自编码器
真大佬啊,论文正文只有两页,打出来就一张纸。
原理
图变分自编码器(Variational Graph Auto-Encoder, VGAE) 是图版本的变分自编码器(Variational Auto-Encoder, VAE):
- 推断网络:视特征矩阵 X 和邻接矩阵 A(但对角元为 1)为可观测变量,每个节点的隐变量 Z 在条件 X, A 下服从正态分布,其参数 $\mu$ 和 $\sigma$ 通过两个共享第一层的两层 GCN(X, A) 得到。
- 生成网络:$p(A_{ij} = 1 | z_i, z_j) = \sigma(z_i^Tz_j)$,其中 $\sigma(\cdot)$ 是 sigmoid 函数
- Z 的先验分布取为标准正态分布
同时提出了一个确定性的模型 图自编码器(Graph Auto-Encoder, GAE) :Z = GCN(X, A), $A = \sigma(ZZ^T)$
实验
实验结果表明 VGAE 和 GAE 能较好地结合节点特征预测无向图上的链接:
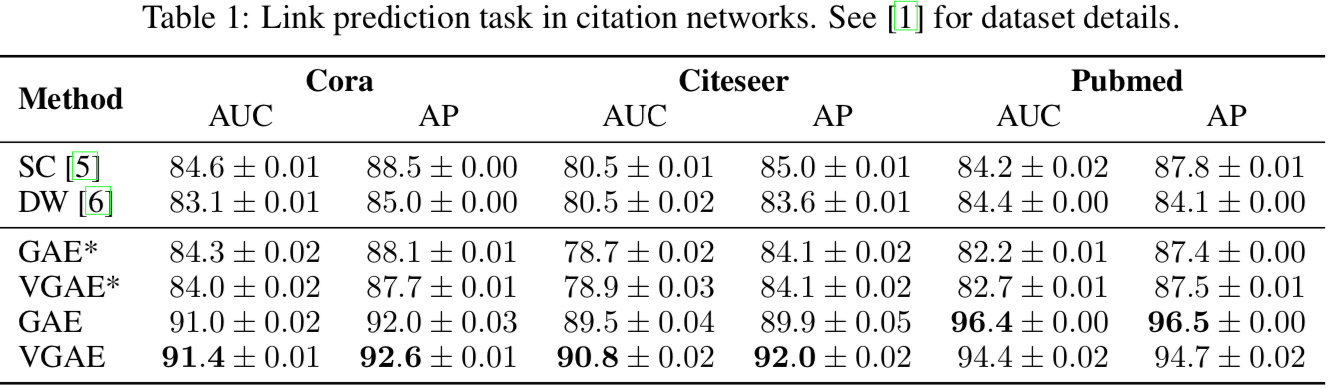
其中 SC 指 Spectral Clustering,DW 指 DeepWalk,这两者都没用到节点特征 X。
所以对应地有 GAE* 和 VGAE* 两个方法,将 X 置为单位矩阵以去掉特征。
但从在 Cora 数据集上学到的隐状态 Z 来看,生成网络采用内积和先验分布取标签正态分布这两点不太搭配,因为内积使得点远离原点,不服从正态分布。

复现
官方pytorch实现中 https://github.com/zfjsail/gae-pytorch/blob/c0b95cac8eb2928d0b5d6d65fee938fe97f60262/gae/optimizer.py
CE 的 pos_weight = n_neg / n_pos 是因为图的稀疏性而做 rescale,否则模型很容易就退化为预测所有边都不存在,损失也能很小。 但是这也带来另一个问题:CE 默认 reduction='mean',分母为 n^2,但实际上经过 pos_weight 后相当于有 2 * n_neg 项了,所以实际的平均值应该再乘以 0.5 * n ^ 2 / n_neg 得到,不知道代码里为什么 norm = (n / n_neg) ^ 2,而且因为这种 norm,KLD 又补救式地再除以了一个 n。
Page Not Found
Try to search through the entire repo.