FastGCN:通过重要性采样快速训练图卷积网络
- 通过对层采样,加速训练 GCN
- 通过重要性采样,降低估计的方差
- 对训练集与测试集的分离更好:训练时,不会用到涉及测试集的边
方法
FastGCN 有如下假设:
- 图:一个无限图中的子图
- 节点:一组独立同分布的样本
- 损失函数与卷积层:节点表示函数的积分(期望)
在这种假设下一个 M 层的GCN(l 为损失函数):
$$H^{(l+1)} = \sigma(\hat A H^{(l)} W^{(l)})$$ $$L = \frac1n \sum\limits_{i=1}^{n} l(H^{(M)}(i, :))$$
可以表示为期望:
$$h^{(l+1)}(v) = \sigma(E_p[\hat A(v, u) h^{(l)}(u) W^{(l)}])$$ $$L = E_p[l(h^{(M)}(v))]$$
于是在除最后一层的每一层均匀采样进行估计:
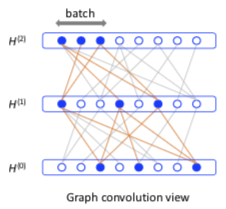
$$H^{(l+1)}(v, :) = \sigma(\frac{n}{t_l} \sum\limits_{j=1}^{t_l} \hat A(v, u_j^{(l)}) H^{(l)}(u_j^{(l)}, :) W^{(l)})$$ $$L = \frac1{t_M} \sum\limits_{i=1}^{t_M} l(H^{(M)}(u_i^{(M)}, :))$$ $$\triangledown \tilde H^{(l+1)}(v, :) = \frac{n}{t_l} \sum\limits_{j=1}^{t_l} \hat A(v, u_j^{(l)}) \triangledown (H^{(l)}(u^{(l)}_j, :) W^{(l)})$$
其中 $t_l$ 表示第 l 层的样本数,n 为全部节点数。
为了减小方差,引入重要性采样(Importance Sampling):
$$h^{(l+1)}(v) = \sigma(E_q[\hat A(v, u) h^{(l)}(u) W^{(l)} \cdot \frac{p(u)}{q(u)}])$$
理论上使方差最小的 q 为
$$q^* \propto \sqrt{E_v[\hat A(v, u)^2]} \cdot |h^{(l)}(u) W^{(l)}| \cdot p(u)$$
但其中 $W^{(l)}$ 每次迭代都会变,与 $h^{(l)}$ 的矩阵乘法也比较耗时。
所以作者将其简化为
$$\hat q \propto \sqrt{E_v[\hat A(v, u)^2]} = ||\hat A(:, u) ||^2$$
也就是节点以正比于 $\hat A$ 矩阵中所在列 2 范数的概率被采样,计算简单且这个分布与层无关。
但作者没能证明这个估计的有效性,只能通过实验说明有效。

实验
首层 Precompute
回顾 GCN 的公式:
$$H^{(l+1)} = \sigma(\hat A H^{(l)} W^{(l)})$$
在输入 $H^{(0)}$ 给定后,整个训练过程中 $\hat A H^{(l)}$ 是个常量,所以这一个矩阵乘法可以省下来。
如图是在 Pubmed 数据集上使用 Precompute 后的结果:准确率(F1)保持,训练时间(秒)明显减少。
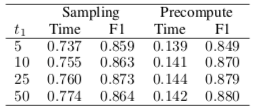
其实这算是对 GCN 的改进,只是 FastGCN 都是采样估计,运算少,这部分改进的作用就明显起来了。
均匀采样与重要性采样的对比
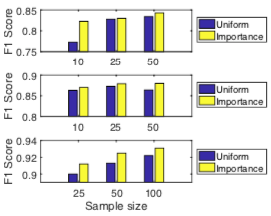
从上到下依次是 Cora, Pubmed 和 Reddit 数据集。
IS 的结果总是更准一些,作者说是因为这方法的方差确实更小。
我觉得更直观地看是因为节点以正比于度的概率被采样,与上层节点有关联的概率更高,因此上层节点更能学到东西。
与 GraphSAGE 和 GCN 的对比
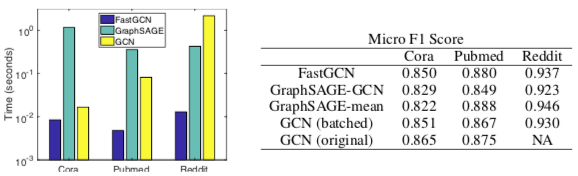
有个 NA 是因为 Reddit 数据集太大,原始的 GCN 作者没法测,所以上面改了个分批版,等于无采样的 FastGCN
- 准确率表现相近
- 速度方面
- 三个数据集一个比一个大、稠密,所以 GraphSAGE 要在 Reddit 上才能体现出对 GCN 的优势
- 在 Pubmed 和 Reddit 数据集上 FastGCN 对 GCN 有数量级的提升(注意时间轴是对数轴)
总结
- 对比 GraphSAGE 是在节点的领域中采样,FastGCN 在层上采样。所以就速度来说,GraphSAGE 对 GCN 是“线性”的改进,FastGCN 是数量级的改进。
- FastGCN 有这样一个缺陷:如果图大而稀疏(这才是现实),相邻层的样本很可能没有关联,导致无法学习。
Page Not Found
Try to search through the entire repo.