神经常微分方程

Hinton 创建的向量学院

2018 NIPS 最佳论文奖

常微分方程（Ordinary Differential Equation, ODE）及其数值解

本文研究以下带初值 h(0) 的 ODE $$\frac{dh(t)}{dt} = f(t, h(t))$$

对 ODE 积分有 $$h(t) = h(s) + \int_s^t f(x, h(x)) dx$$ 由积分中值定理 $$h(t) = h(s) + (t - s) \cdot f(x, h(x)), x \in [s, t]$$

写成递推式 $$h(t + \Delta t) = h(t) + \Delta t \cdot f(x, h(x))$$ 如果能估计出各步的 $f(x, h(x))$，由 h(0) 开始就可以逐步推出 h(T)

此外，如果步长为负则得到反向的递推公式 $$h(t - \Delta t) = h(t) - \Delta t \cdot f(x, h(x))$$ 可由 h(T) 逐步推出 h(0)

ODE Solver 举例

各种 ODE Solver 对 $f(x, h(x))$ 进行了不同的估计：

Euler 法：$f(x, h(x)) \approx f(s, h(s))$
中点法（RK2）：$f(x, h(x)) \approx \frac{1}{2} \cdot (f(s, h(s)) + f(t, h(s) + (t - s) \cdot f(s, h(s))))$

此外还有 Runge-Kutta (RK4) 和 Adams-Bashforth 等。

以 Euler 法为例，当步长 $\Delta t$ 较小时，可以用 $$h(t + \Delta t) \approx h(t) + \Delta t \cdot f(t, h(t))$$ 从 h(t) 的初值开始一步步估算出终值。

伪码如下（步长不必固定）：

for dt in dts:
    h += dt * f(t, h)
    t += dt

NeuralODE

注意到残差网络、RNN 网络的 decoder、归一化流的模型与 Euler 法有相同的形式： $$h_{t+1} = h_{t} + f(h_t \theta_t)$$

digraph {
    label="ODE Solver";
    rankdir=LR;
    node [shape=none];
    h0 [label="h(0)"]; ht [label="h(T)"];
    subgraph cluster_ode {
        label="t=0";
        dot [label="."];
        f [shape=box, label="f * dt"];
        plus [shape=circle, label="+"];
        dot -> f [label="h, t"];
        f -> plus;
        dot -> plus [constraint=false];
    }
    h0 -> dot;
    t1 [label="...", shape=none];
    tt [label="t=T", shape=box];
    plus -> t1 -> tt ->  ht;
}

digraph {
    label="两层 ResNet 的前向计算";
    rankdir=LR;
    node [shape=none];
    x; y;
    subgraph cluster_l1 {
        label="ResNet Layer 1";
        dot1 [label="."];
        conv1 [shape=box, label="conv"];
        node [shape=circle];
        plus1 [label="+"];
        relu1 [label="σ"];
        dot1 -> conv1 -> plus1 -> relu1;
        dot1 -> plus1 [constraint=false];
    }
    l2 [shape=box, label="ResNet Layer 2"];
    x -> dot1;
    relu1 -> l2;
    l2 -> y;
}

假设这些离散的网络层（$\Delta t=1$）之间还存在无穷多的层，使步长 $\Delta t$ 可以无穷小以致 t 连续，则模型可写成 ODE 的形式： $$\frac{dh(t)}{dt} = f(h(t), t, \theta)$$ 输入层是这个 ODE 的初值 h(0)，输出层就是解 h(t) 在 t=T 时的值 h(T)。
而本身的模型就是这个带初值常微分方程定义的连续网络的离散化。

ResNet and Neural ODE

建模为 ODE 的好处：

少量参数就可以建模复杂的动力系统
网络深度是自适应的，通过数值误差的阈值进行控制，可在精度与速度之间权衡
中间任意连续时刻的隐状态都是可知的

参数学习：伴随法（Adjoint Method）

用普通的误差反向传播也可以学习模型参数，但当中间的时间步很多时，需要保存大量的中间梯度，造成内存问题，数值误差的影响也不受控。

于是作者通过伴随法的应用，绕过 ODE Solver 得到了误差对参数的梯度，并且达到了常数级的空间复杂度。

定义伴随状态（Adjoint State） $$a_g(t) = \frac{\partial{L}}{\partial{g(t)}}$$

由链式法则 $$ a_g(t) = \frac{\partial{L}}{\partial{g(t + \epsilon)}} \cdot \frac{\partial{g(t + \epsilon)}}{\partial{g(t)}} = a_g(t + \epsilon) \cdot \frac{\partial{g(t + \epsilon)}}{\partial{g(t)}}$$

有 $$\begin{aligned} \frac{da_g(t)}{dt} &= \lim\limits_{\epsilon -> 0^+} \frac{a_g(t+\epsilon) - a_g(t)}{\epsilon} \\ &= \lim\limits_{\epsilon -> 0^+} a_g(t+\epsilon) \cdot \frac{\frac{\partial{g(t) - g(t+\epsilon)}}{\partial{g(t)}} }{\epsilon} \\ &= - a_g(t) \cdot \frac{\partial{g'(t)}}{\partial{g(t)}} \end{aligned}$$

令 $g(t) = (h(t), \theta, t)^T$ 代入 $$\begin{aligned} \frac{da_g(t)}{dt} &= - (a_h(t), a_\theta(t), a_t(t)) \cdot \begin{pmatrix} \frac{\partial{h'(t)}}{\partial{h(t)}} & \frac{\partial{h'(t)}}{\partial{\theta}} & \frac{\partial{h'(t)}}{\partial{t}} \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \\ &= -( a_h(t) \cdot \frac{\partial{h'(t)}}{\partial{h(t)}}, a_h(t) \cdot \frac{\partial{h'(t)}}{\partial{\theta}}, a_h(t) \cdot \frac{\partial{h'(t)}}{\partial{t}} ) \end{aligned}$$

于是得到了三个 ODE（原文构造了一个增广矩阵按一个 ODE 一起算，这里便于说明拆成了三个 ODE） $$\begin{cases} \frac{da_h(t)}{dt} = - a_h(t) \cdot \frac{\partial{f(h(t), t, \theta)}}{\partial{h(t)}} \\ \frac{da_\theta(t)}{dt} = - a_h(t) \cdot \frac{\partial{f(h(t), t, \theta)}}{\partial{\theta}} \\ \frac{da_t(t)}{dt} = - a_h(t) \cdot \frac{\partial{f(h(t), t, \theta)}}{\partial{t}} \end{cases}$$

对应的最终时刻的值

$a_h(T) = \frac{\partial{L}}{\partial{h(T)}} $ 可由损失函数的定义计算出
作者说“setting $a_\theta(T) = 0$”没说为什么，我猜是因为优化问题最终就是要让损失函数相对参数的梯度为0
$a_t(T) = \frac{\partial{L}}{\partial{t}} |_T = \frac{\partial{L}}{\partial{h}} \cdot \frac{\partial{h}}{\partial{t}} |_T = a_t(T) \cdot f(h(T), T, \theta)$

于是反向递推可得到损失函数相对于初始时刻的状态、模型参数和时间 t 的梯度 $a_h(0), a_\theta(0), a_t(0)$。

以优化$\theta$为例，记$\alpha = \frac{\partial{L}}{\partial{h(t_N)}}$，$\beta$为学习率，因为 $$\frac{\partial{L}}{\partial{\theta(t_0)}} = \frac{\partial{L}}{\partial{\theta(t_N)}} - \int_{t_N}^{t_0} \alpha \cdot \frac{\partial{f(\theta)}}{\partial{\theta(t)}} dt$$ 其中第一项按前面设置是0，$\alpha \cdot \frac{\partial{f(\theta)}}{\partial{\theta(t)}}$可以在使用f(*args).backward(alpha)后通过theta.grad得到，而且很多时候神经网络里的参数都是可以让输出值随便线性调整的（最后一层不是非线性），所以时间间隔具体是多少也不重要，省略了也可以。

监督学习

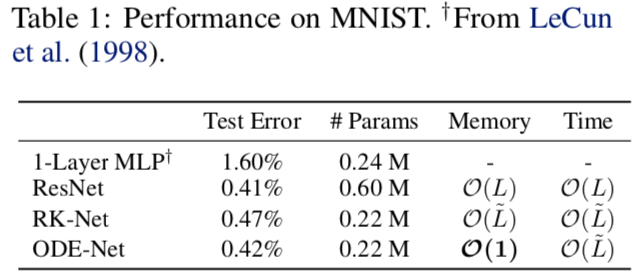
Neural ODE on MNIST

用更少参数达到了 ResNet 相似的准确度
达到了常数级的空间复杂度
- RK-Net 是用 Runge-Kutta 前向估算 ODE，但优化时仍用的 BP 算法，所以内存还是高
时间复杂度都跟网络深度一致，但 ODE-Net 的深度是自适应的，无法直接比较（但后面实验表明 ODE-Net 更快）

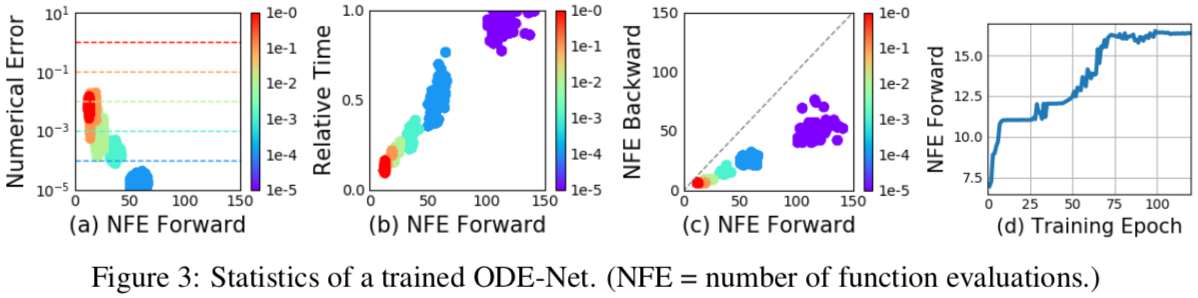
Error Control in ODE-Nets

a 表明 ODE 的数值解的误差阈值与计算量成反比，而计算量与运行时间成正比（b），所以可以训练时减小误差阈值以提高精度，测试时放松阈值以提升速度；
反向计算梯度时计算量比前向计算还少一半，作者认为是反向传播时评估节点可能更少

连续型归一化流

生成时间序列模型

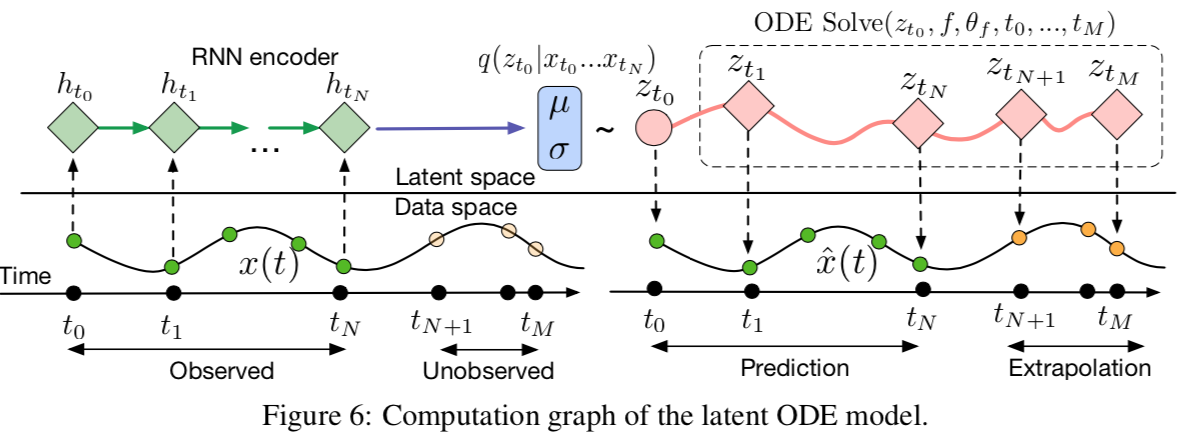
ODE Time-Series Model