因果模型的抽象

应用
数据
方法

摘要

我们考虑了一系列逐步严格的因果模型抽象的定义。

首先是 Rubenstein 等人引入的概率因果模型的精确变换
其次是确定因果模型的统一变换，该变换防止了特殊构造的分布掩盖模型的差异；
再次是抽象，通过低层到高层的映射确定了干涉的价值；
最后是强抽象，在可行的干涉之外，还考虑了所有潜在的干涉。

最后我们指出了将微变量组合成宏变量的过程，以及 Rubenstein 等人考虑的所有例子都是强抽象概念的实例。

概率因果模型的基础知识

A signature S: (U, V, R)

U: 外部变量（exogenous variables）。U 的一组取值 $\vec{u}$ 也称一个环境。
V: 内部变量（endogenous variables）
R: 随机变量的取值域

本文限制模型是递归（无环）的，即 $$\forall \vec{u} \exists< \text{ as a partial order } \text{ that Y depends on X in } \vec{u} \text{ if X < Y }$$ 如果这个偏序关系独立于 $\vec{u}$，则模型是强递归的 .

基本因果模型：(S, F)

F: 随机变量方程，如 X = Y + U

因果模型：(S, F, I) = (M, I)

I: 可行的干涉（Intervention）的集合

干涉

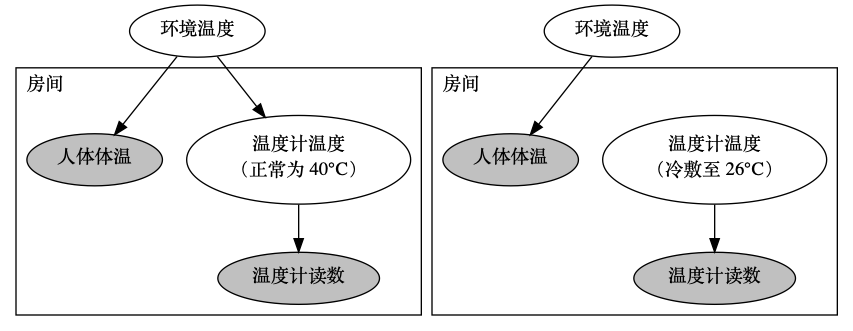
干涉的例子

对因果模型施加一个干涉 $\vec{X} \leftarrow \vec{x}$，则 F 中所有的 $\vec{X}$ 被替换为 $\vec{x}$、$\forall Y \notin \vec{X}$ 不变，记为 $F^{\vec{X} \leftarrow \vec{x}}$。因此这是一个新的因果模型 (S, $F^{\vec{X} \leftarrow \vec{x}}$, I)。

因果命题 $\phi: [\vec{Y} \leftarrow \vec{y}]\varphi$
其中 $\varphi$ 是一些原始事件的布尔组合，比如 $\varphi = {X_1 = x_1, X_2 = x_2}$

该命题表示当 $\vec{Y} \leftarrow \vec{y}$ 时 $\varphi$ 成立。

但这个命题成立与否也是与模型和具体环境有关的，所以进一步用 $(M, \vec{u}) \text{ |= } \phi$ 表示在模型 M 中环境 $\vec{u}$ 下 $\phi$ 成立。

概率因果模型：(S, F, I, Pr) = (M, Pr)

Pr: Contexts 的分布律（A probability on contexts）

概率因果模型中的 (S, F, I) 称为确定因果模型。

UEV 引理

UEV：因果模型的每个内部变量都唯一依赖于一个不同的外部变量，则称这因果模型是带 Unique Exogenous Variables (UEV) 的。

UEV

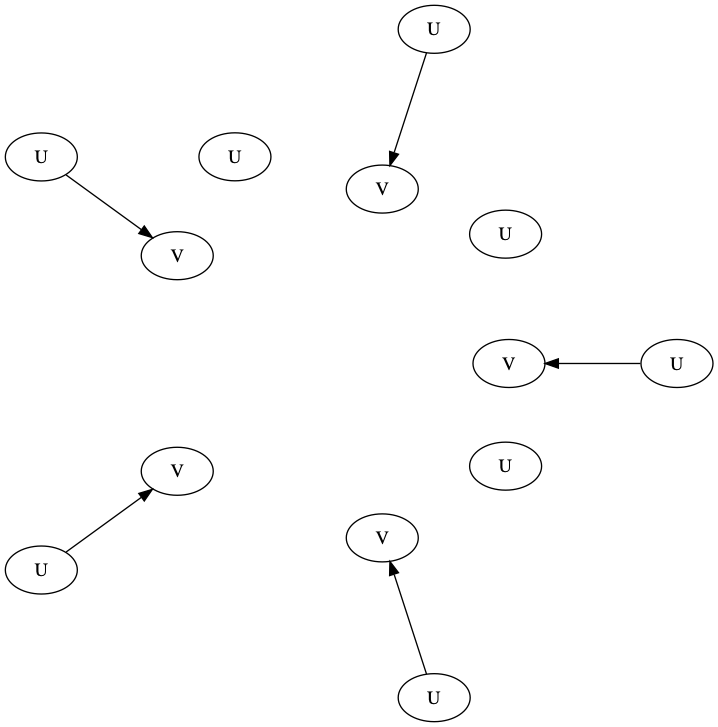
UEV 引理：任一概率因果模型都有一个带 UEV 的概率因果模型与之等价。

因为 UEV 引理，本文只考虑带 UEV 的概率因果模型。这样环境变量的分布律 Pr 就可视为所有变量的分布律。

概率因果模型等价，即对概率因果模型 M = ((U, V, R), F, I, Pr) 与 M' = ((U', V', R'), F', I', Pr')，有

V = V'
I = I'
$ R(Y) = R'(Y), \forall Y \in V$
任一因果命题在 M 与 M' 中有相同概率成立，

因果模型的逐步抽象

精确变换（Exact Transformation）

对概率因果模型 $(M_L, Pr_L)$ 和 $(M_H, Pr_H)$ $$ \tau: R_L(V_L) \rightarrow R_H(V_H) $$ $$ \omega: I_L \rightarrow I_H \text{ 是一个保序的满射} $$ $$ Pr^{\omega(\vec{Y} \leftarrow \vec{y})}_H = \tau(Pr^{\vec{Y} \leftarrow \vec{y}}_L) $$ 称 $(M_H, Pr_H)$ 为 $(M_L, Pr_L)$ 的 $(\tau-\omega)$ 精确变换（Exact $(\tau-\omega)$-transformation）。

例子：宣传与投票

应用：

有边缘变量的模型（可以简化？）；
成组聚合变量，将低层模型转为高层模型（如前面的例子）；
将随时间变化的动态过程转为均衡态。

统一变换（Uniform Transformation）

可构造两个彼此为精确变换但无关的模型，说明精确变换这个抽象没触及本质。因此针对分布律，提出了统一变换。

定义

对确定因果模型 $M_L$ 和 $M_H$、保序满射 $\omega: I_L \rightarrow I_H$、$\tau: R_L(V_L) \rightarrow R_H(V_H)$，称 $M_H$ 是 $M_L$ 的 $(\tau-\omega)$ 统一变换（Uniform $(\tau-\omega)$-transformation），如果 $\forall Pr_L \exists Pr_H \text{ that } (M_H, Pr_H)$ 是 $(M_L, Pr_L)$ 的 $(\tau-\omega)$ 精确变换。

意义

既然对特定的 $\omega$，对任意 $Pr_L$ 都能找到对应的 $Pr_H$，使高层模型是低层模型的精确变换，那么两个分布就是函数关系：

推论：如果 $M_H$ 是 $M_L$ 的 $(\tau-\omega)$ 统一变换，则有函数 $\tau_U: R(U_L) \rightarrow R(U_H) \text{ that } \forall Pr_L on R(U_L), (M_H, \tau_U(Pr_L))$ 是 $(M_L, Pr_L)$ 的$(\tau-\omega)$ 精确变换。

判定

定理：在定义条件下，$M_H$ 是 $M_L$ 的统一变换的充要条件为存在 $R(U_L) \rightarrow R(U_H)$ 的变换与 $\tau$ 兼容。

所谓 $\tau': R(U_L) \rightarrow R(U_H) 与 \tau: R(V_L) \rightarrow R(V_H)$ 兼容，定义为 $$ \forall \vec{Y} \leftarrow \vec{y} \in I_L \text{ and } \vec{u}_L \in R(U_L) $$ $$ \tau(M_L(\vec{u}_L, \vec{Y} \leftarrow \vec{y})) = M_H(\tau'(\vec{u}_L), \omega(\vec{Y} \leftarrow \vec{y})) $$

性质：可结合

定理：$M_H$ 是 $M_I$ 的 $(\tau_1-\omega_1)$ 统一变换
$M_I$ 是 $M_L$ 的 $(\tau_2-\omega_2)$ 统一变换
则 $M_H$ 是 $M_L$ 的 $((\tau_1 \circ \tau_2)-(\omega_1 \circ \omega_2))$ 统一变换

抽象（Abstraction）

因为前面的定义对 $\tau$ 没限制，可以因此构造出反直觉的或者高层模型反而更繁琐的例子，故又针对 $\tau$ 提出了 $\tau$-抽象。

$\tau$ 是满射
存在满射 $\tau_U: R(U_L) \rightarrow R(U_H)$ 与 $\tau$ 兼容
$I_H = \omega_{\tau}(I_L)$

则 $M_H$ 是 $M_L$ 的 $\tau$-抽象。

不同于精确变换和统一变换，$\tau$-抽象是因果模型之间的一个关系，因为由 $\tau$ 可确定 $\omega$（？），便不再需要指定分布。

强抽象（Strong Abstraction）

如果 $(M_H, I^{\tau}_H)$ 是 $(M_L, I^{\tau}_L)$ 的 $\tau$-抽象，且 $I^{\tau}_H$ 包含了所有高层的干涉，则说 $M_H$ 是 $M_L$ 的 $\tau$-强抽象。

这是一个基本因果模型间的关系。

最后提出了 $\tau$-强抽象的一种特殊情况 $\tau$-连续强抽象，作者认为这种抽象可能的用处很广，因为 RW+ 所提的三个应用方向都是 $\tau$-连续强抽象，但相关定理与性质本文还未能证明。