用颠倒强化学习训练智能体
这篇文章主要是颠倒强化学习(Upside-Down Reinforcement Learning, UDRL)的实现细节和实验效果。
详细的理论见另一篇论文:《颠倒强化学习:不要预测回报,直接得到动作》。
当前强化学习的三个方向
1. 值函数
在当前状态 Observation 下,对所有可能的 Action 取值,代入 Q 函数估算期望回报 $v = Q(o, a)$,取其中最大化期望回报的动作:$\mathop{\arg\max}\limits_{a \in A} Q(o, a)$
digraph {
label="Q-value Function";
labelloc=t;
rankdir=LR;
Q [shape=box, fillcolor=grey, style=filled];
node [shape=none];
{ Observation Action } -> Q -> "Value\n(expected return)";
}
其中 Q 函数又称动作值函数,常用的还有状态值函数 V(o) 和 优势函数 A(o, a)。
本文实验基准之一就是基于 Q 函数的 DQN。
2. 策略梯度
将策略函数作为优化点,以期望回报为目标函数,做梯度上升,使策略越来越优。
通常与值函数结合,即 Actor-Critic 算法。
本文实验基准之一就是基于 AC 算法的 A2C(Advantage Actor-Critic,同步版 A3C)。
3. 进化
如之前介绍过的论文《权重无关神经网络》 就使用进化的方式做架构搜索。
4. 行为函数
在当前状态 Observation 下,将期望的时间与回报 Command 代入 B 函数,得到动作 Action:$a = B(o, c)$
digraph {
label="Behaviour Function";
labelloc=t;
rankdir=LR;
B [shape=box, fillcolor=grey, style=filled];
node [shape=none];
{ Observation "Command\n(desired return & horizon)" } -> B -> Action;
}
与前面值函数方法相比好像旋转了下,所以作者把这套方法叫颠倒强化学习(Upside-Down Reinforcement Learning, UDRL)。
比如下面这样一个马尔可夫决策过程(Markov Decision Process, MDP):
digraph {
rankdir=LR;
s0 -> s1 [label="a1, r=2"];
s1 -> s3 [label="a3, r=-1"];
s0 -> s2 [label="a2, r=1"];
}
可用 B 函数表达如下(前三列都是输入,Action 是输出):
| State | Desired Return | Desired Horizon | Action |
|---|---|---|---|
| s0 | 2 | 1 | a1 |
| s0 | 1 | 1 | a2 |
| s0 | 1 | 2 | a1 |
| s1 | -1 | 1 | a3 |
UDRL 算法
digraph {
rankdir=LR;
node [shape=box];
cmd [label="cmd(1)"];
tr [label="trace(T)"];
node [fillcolor=grey, style=filled];
buf [label="Replay Buffer"];
B;
buf -> cmd [label="Sample\nCommands"];
cmd -> B [label="+all(1)"];
buf -> B [label="Train"];
B -> tr [label="Repeat till done"];
buf -> tr [label="Update", dir=back];
}
- Replay Buffer 中只保留固定数目的最高回报轨迹,这样网络能逼近出高回报的策略;
- 训练过程就是使 B 函数逼近 Replay Buffer。详见我另一篇论文的笔记,本论文原文中也有;
- 命令采样是从 Replay Buffer 中抽一组最高回报的轨迹,取 horizon(1) = 平均时长 ,desire(1) = 平均回报 + $\gamma \cdot$ 回报标准差,其中 $\gamma \sim U(0, 1)$;
- 对采样出的每一个命令 cmd(1),与初始状态 all(1) 一起输入 B 得到动作并更新 cmd(t) 和 all(t),一直重复直至该回合结束,得到一条轨迹,加入到 Replay Buffer。
实验效果

-
Gym RL Library 中的 LunarLander-v2。控制飞船在月球表面降落,每一步都可以得到当前所有状态的值和该步回报。典型的马尔可夫环境;
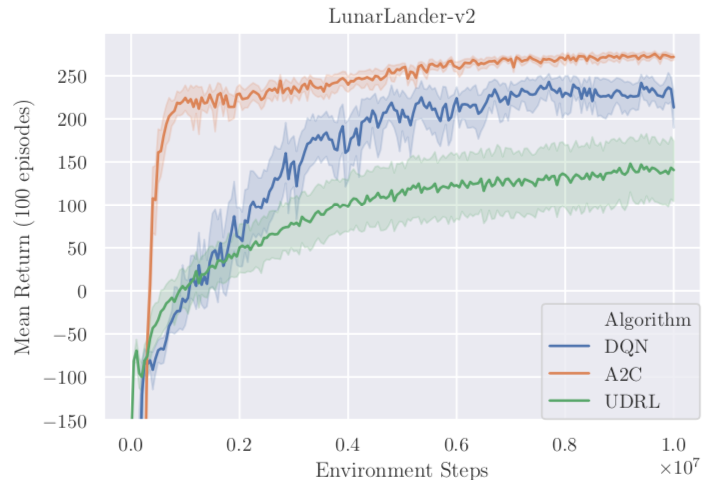
-
LunarLanderSparse。将 LunarLander-v2 的回报改为累积到最终才得到,中间过程无回报。非马尔可夫过程。
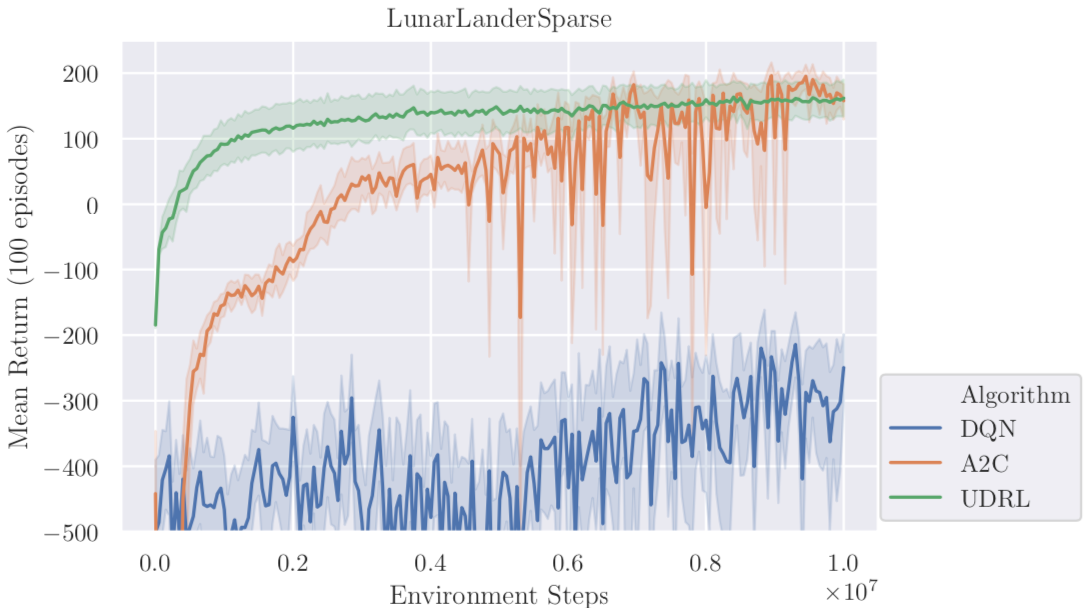
-
ViZDoom 中的 TakeCover-v0。第一人称射击游戏,存在不可见状态。非马尔可夫环境。
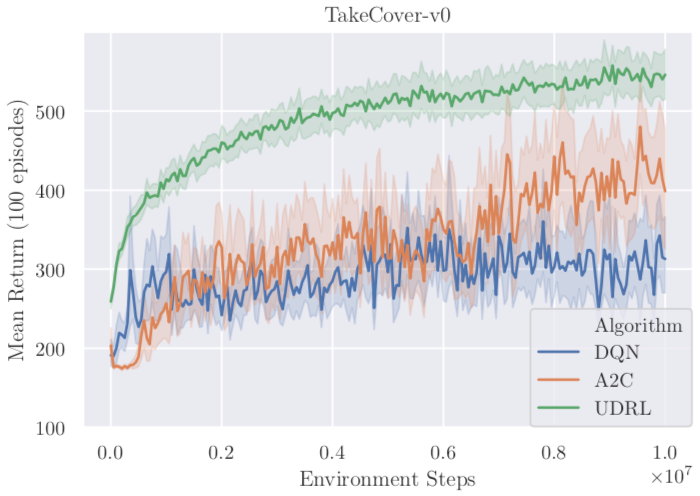
结论:
- 在马尔可夫环境中,经典的 RL 方法表现更好;
- 在非马尔可夫环境中,UDRL 表现更好;
- 回报的结构对结果影响很大。UDRL 在 Sparse 结构中的表现反而比调整前更好。
后面还有一个目标收益与实际收益相关性研究的图表,但数据样本看起来并不多,在 LunarLanderSparse 上训练的两个智能体还呈现了不同的特点,作者自己也说不清为什么。所以不解读了。
Page Not Found
Try to search through the entire repo.