DS证据理论与主观逻辑
基本概念
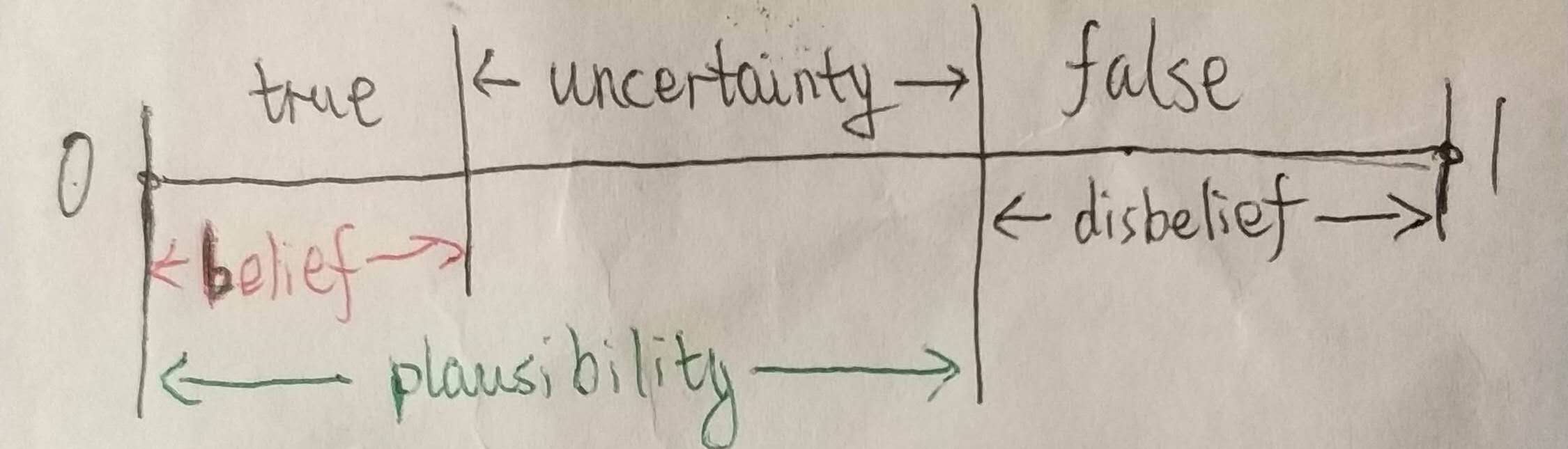
对于单一假设,引入不确定性(Uncertainty)后,产生信度(Belief)与似然(Plausibility)的概念。
对 N 个对立事件(要求其并必然发生),考虑不确定性可以有 $2^N$ 个假设,每个假设对应事件幂集中的一个元素,除空集元素必须分配为 0 以外,其它元素可分配一个和为一的概率,称为 Mass,表示该假设的可能性。
一个 N = 3 的例子:有灯能发出 R, G, B 三种颜色的光,于是有以下 8 个假设。观测者观测后对每个假设分配 mass 值:
| 假设 | mass | 含义 |
|---|---|---|
| $\emptyset$ | 0 | 不发光 |
| {R} | 0.35 | 发 R 光 |
| {G} | 0.15 | 发 G 光 |
| {B} | 0.25 | 发 B 光 |
| {R, G} | 0.05 | 发 R 光或 G 光 |
| {G, B} | 0.04 | 发 G 光或 B 光 |
| {B, R} | 0.06 | 发 B 光或 R 光 |
| {R, G, B} | 0.1 | 发某光 |
- 例如 mass({RG) = 0.05 表示有 5% 可能确定要么发 R 光要么发 G 光,但不能确定具体发 R 光还是发 G 光。
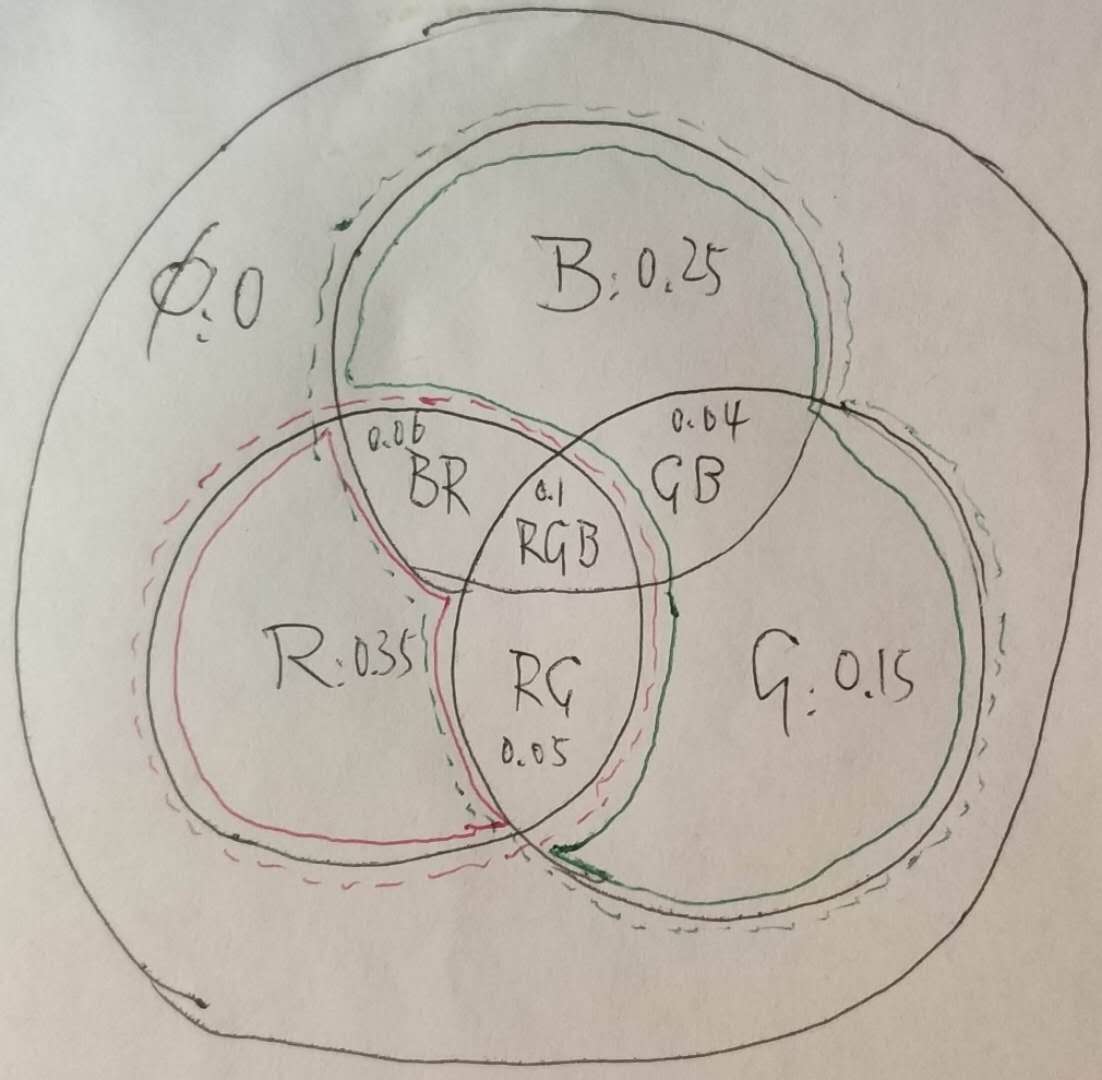
根据每个假设的 Mass 值可以计算该假设的信度和似然。
- 信度 = 该假设所有子集的 mass 之和
- 似然 = 所有与该假设相交非空的集合的 mass 之和
- 概率 $\in$ [信度, 似然] = 信任区间
如上图中
- Belief(R) = 红色实线部分 = 0.35
- Plausibility(R) = 红色虚线部分 = 0.56
- Belief(GB) = 绿色实线部分 = 0.44
- Plausibility(GB) = 绿色虚线部分 = 0.65
主观逻辑(Subjective Logic)
概率 = 信度 + 不确定性 * 先验概率
先验概率(Base rate)指无证据时假设成立的概率
例如对上面的例子,引入先验概率 (pri(R), pri(G), pri(B)) ~ (0.5, 0.3, 0.2),则结合观测有
P(R) = mass(R) + mass(RG) * pri(R|RG) + mass(BR) * pri(R|BR) + mass(RGB) * pri(R) = 47.4%
同理可计算 P(G) = 22.3%, P(B) = 30.3%。
Dempster-Shafer 证据合成
多个观测者各自给出不同的 mass 分配后可通过 DS 合成规则将其合并为一个新的 mass 分配,其中任一非空假设的新 mass 值与分属于不同观测者,但相交为该假设的原 mass 值乘积之和成正比。
| 假设 | 观测1 | 观测2 | 合并(未归一化) | 合并 |
|---|---|---|---|---|
| $\emptyset$ | 0 | 0 | 0 | 0 |
| {R} | 0.35 | 0.3 | 0.261 | 0.488 |
| {G} | 0.15 | 0.2 | 0.11 | 0.206 |
| {B} | 0.25 | 0.2 | 0.1575 | 0.295 |
| {R, G} | 0.05 | 0.05 | 0.015 | 0.003 |
| {G, B} | 0.04 | 0.05 | 0.013 | 0.002 |
| {B, R} | 0.06 | 0.05 | 0.017 | 0.003 |
| {R, G, B} | 0.1 | 0.15 | 0.015 | 0.003 |
例如 mass(RG) ∝ mass1(RG) * mass2(RG) + mass1(RG) * mass2(RGB) + mass1(RGB) * mass2(RG) = 0.015
Page Not Found
Try to search through the entire repo.