进化算法
与传统的基于微积分的方法和穷举方法等优化算法相比,进化计算是一种成熟的具有高鲁棒性和广泛适用性的全局优化方法,具有自组织、自适应、自学习的特性,能够不受问题性质的限制,有效地处理传统优化算法难以解决的复杂问题。
遗传算法(Genetic Algorithm, GA)
遗传算法是一个框架,包含以下循环的三步
- 选择。最简单的一步,评估当前一代每个个体的表现,选取(或按概率选取)表现最好的一批作为父代
- 交叉。最重要的一步,根据父代个体的性质生成新的子代,比如每一位特征都随机选一个父代进行继承
- 变异。对子代随机变换,以保持多样性,避免陷入局部最优
比如2021年的SHARE算法中搜索层次化联邦学习的分组结构时,就用到了遗传算法。 具体是定义了增加节点、删除节点和替换节点三种交叉变异的操作,既从父代继承基本的结构,又产生出新的变化。
差分进化算法(Differential Evolution, DE)
$$ X_i' = \text{better}(X_i, [ \text{random}(x_{ij}, x_{rj} + \alpha ( x_{sj} - x_{tj} )) ]) $$
- 变异:$X_i' = X_r + \alpha (X_s - X_t)$。随机选择个体$X_s$和$X_t$计算,将差缩放后加到另一个随机个体$X_r$上,得到变异结果
- 交叉:random($x_{ij}, x_{ij}'$)。对每一位,随机选择是否保留变异结果,产生新一代个体$X_i'$
- 选择:better($X_i, X_i'$)。在上一代$X_i$和新一代$X_i'$之间选好的留下
比如2017年的单像素攻击中用差分进化算法搜索攻击像素点,可调用scipy.optimize.differential_evolution实现。
进化策略(Evolution Strategy, ES)
进化策略主要假设个体样本满足一个高斯分布,通过循环选择精英样本、更新分布、重新采样不断得到更好的样本。
最简单的情况就是方差固定,取最优样本作为下一代样本分布均值。 如图,其中蓝点为样本,绿点为样本均值,红点为最优样本。
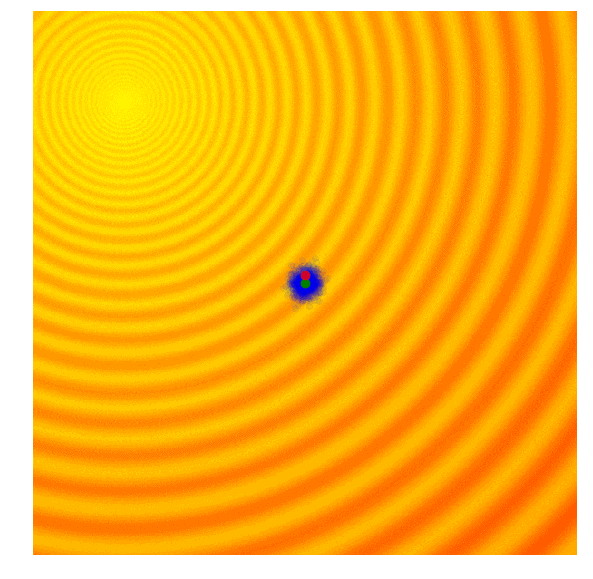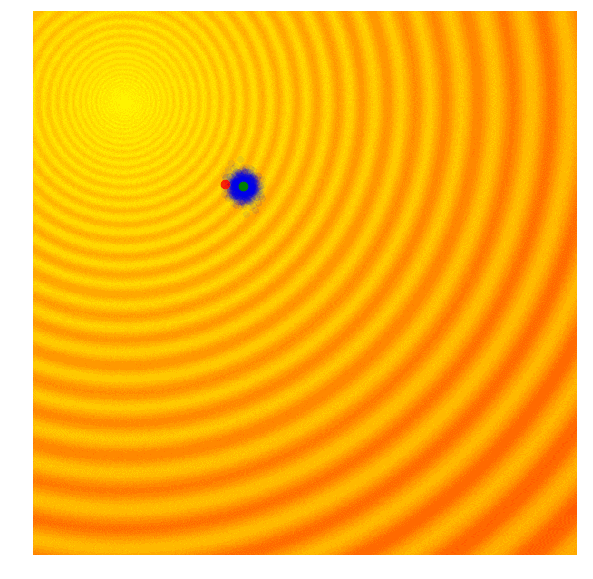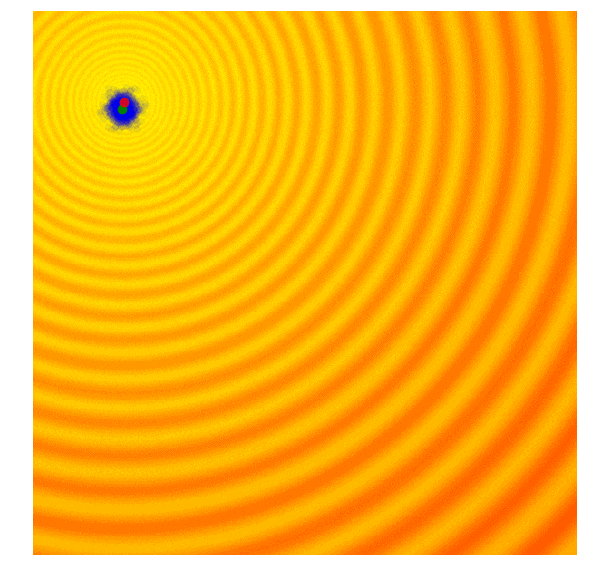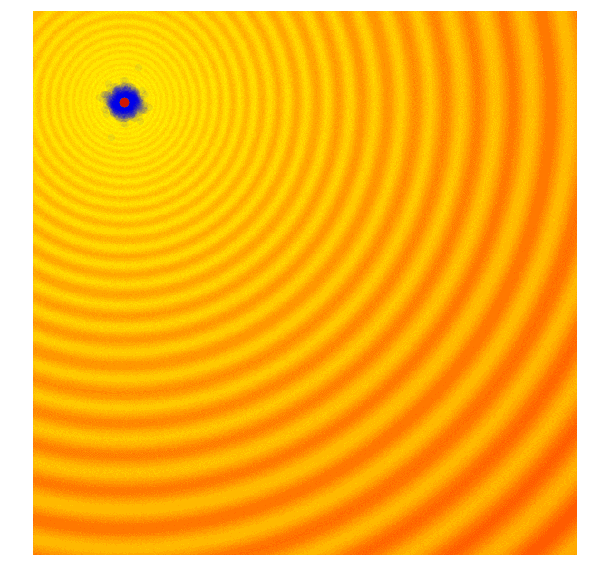
ES的一个变形是自然演化策略(Natural Evolution Strategy, NES),认为应该利用每个个体的表现信息寻求整体优化,而不是只保留精英个体鼓励个体优化。 因此提出更新分布时应该最大化表现的期望$\mathbb{E}_{x \sim p(\cdot | \theta)} [f(x)]$。
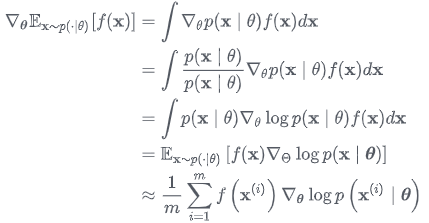
最终导出的算法其实跟强化学习中策略梯度是一样的。
协方差矩阵自适应进化策略(Covariance Matrix Adaptation Evolution Strategy, CMA-ES)
CMA-ES对于ES的改进主要在于对分布方差的控制,其中协方差矩阵CM代表对方向的控制,自适应A代表对步长的控制。
公式比较多可参考原论文,直观感受如图:
CMA-ES可以控制搜索空间的形状和大小,这样收敛快又不会错过最优点。
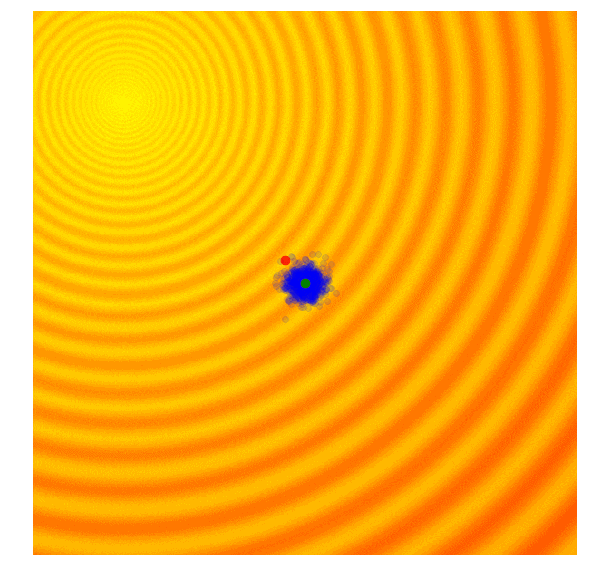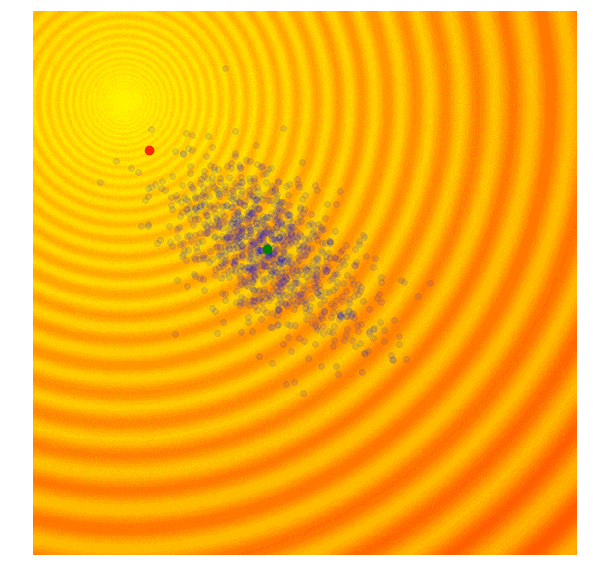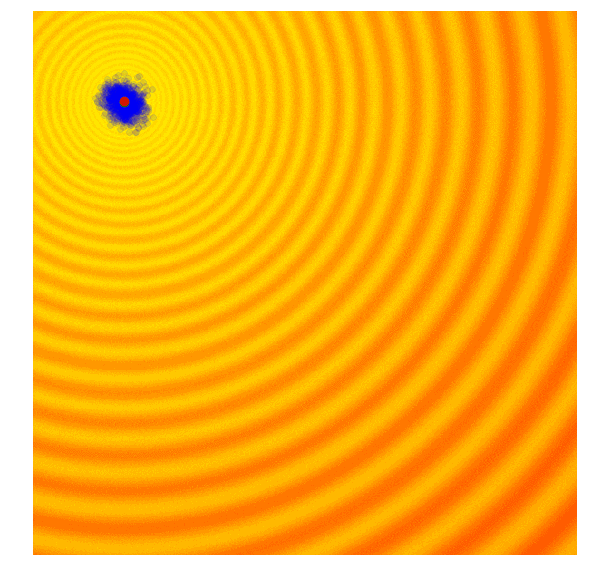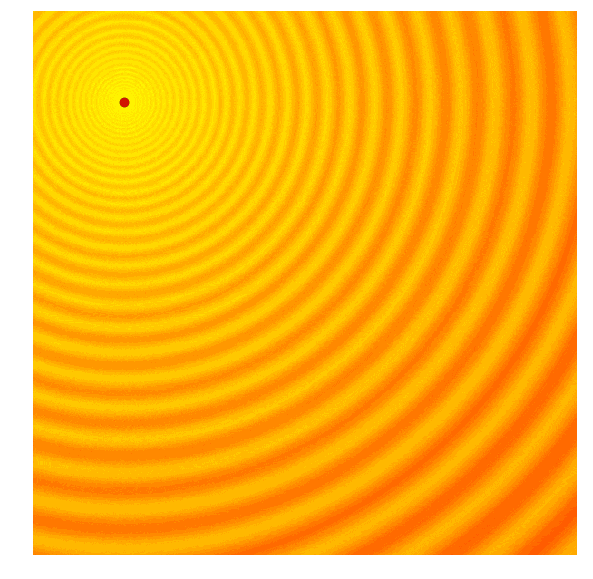
算法实现见pycma这个库。
Page Not Found
Try to search through the entire repo.