概率论与数理统计
联合分布函数,条件概率,乘法定理,全概率公式,贝叶斯公式,边缘分布,条件分布,随机变量的函数的分布,相互独立,期望,方差,协方差,标准化变量,相关系数,切比雪夫不等式,柯西-施瓦茨不等式,协方差矩阵,n维正态分布

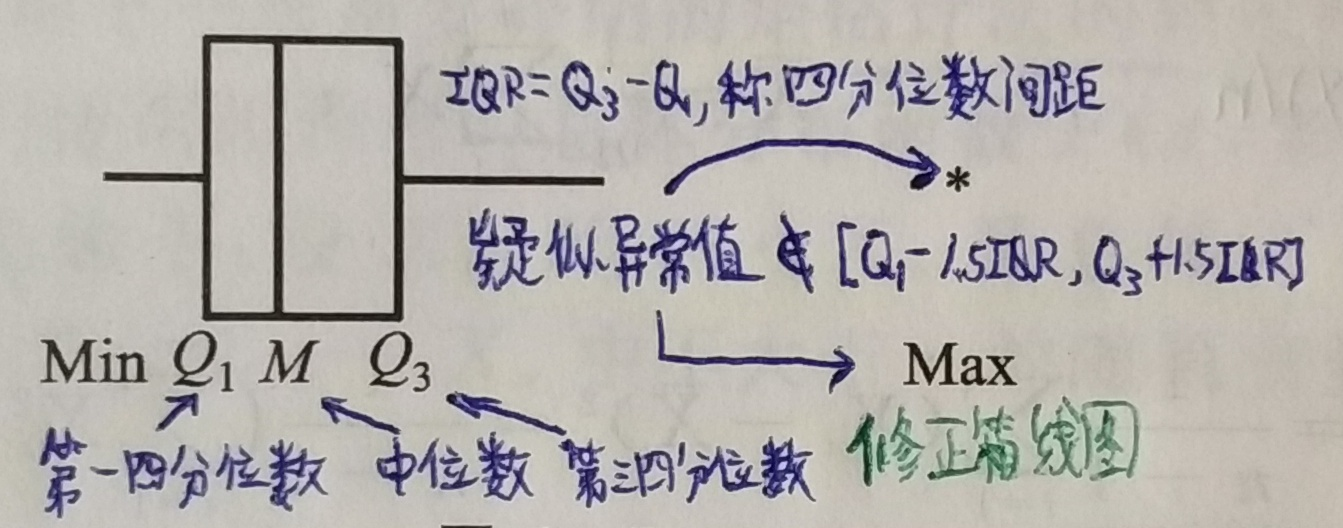
- 顺序统计量:抽象一组数据后按值排序作为各分量的值,显然就不相互独立。
- 中位数:顺序统计量里正中靠右那个值。
- 极差:最大的 - 最小的
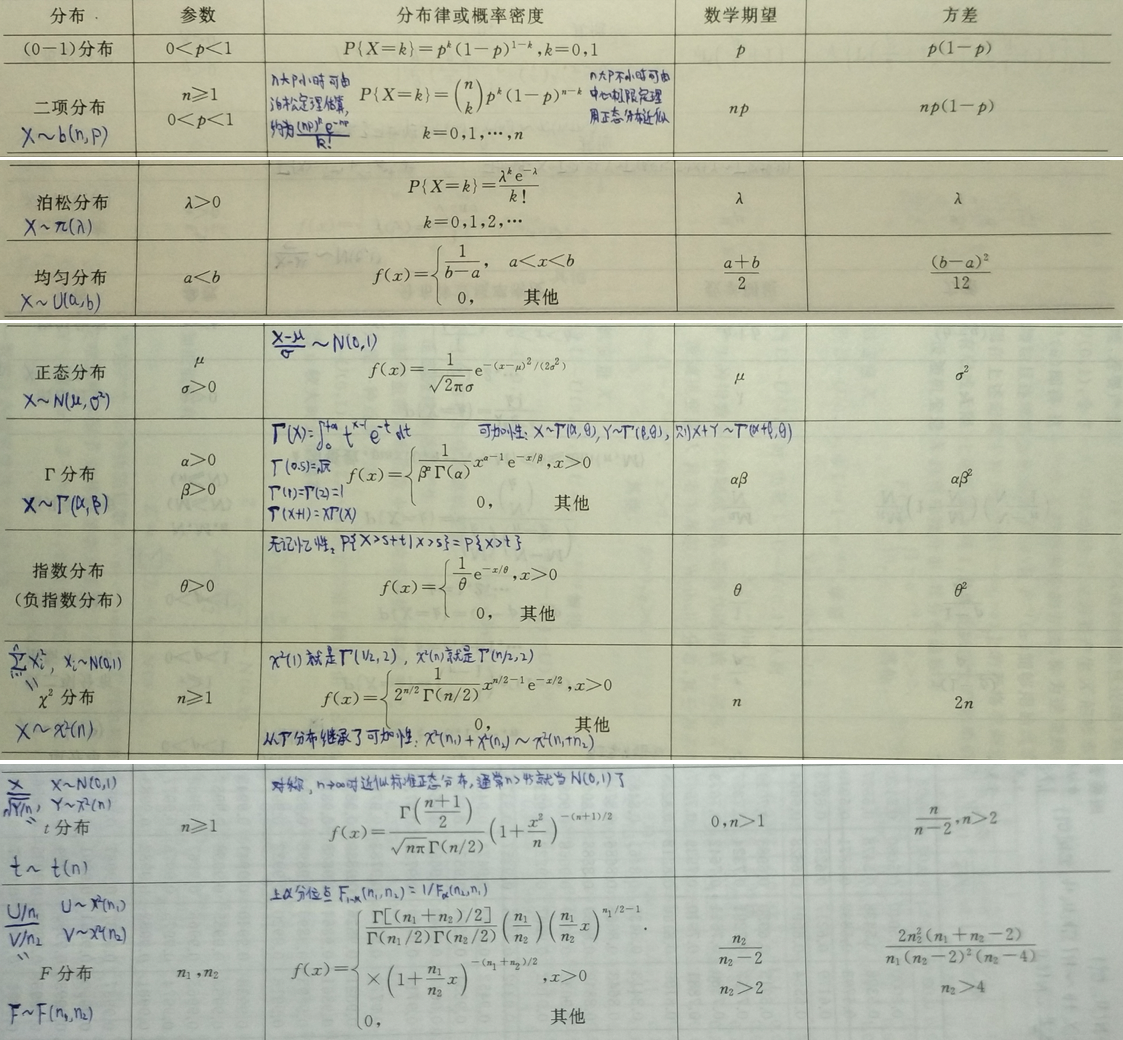
常用概率分布表
(0, 1)分布,两点分布,二项分布,泊松分布,均匀分布,正态分布,高斯分布,伽马分布,Γ分布,指数分布,X2分布,t分布,F分布
大数定律与中心极限定理
切比雪夫不等式,依概率收敛, 大数定律,切比雪夫大数定理,辛钦大数定理,弱大数定理,伯努利大数定理, 中心极限定理,李雅普诺夫定理,列维-林德伯格定理,棣莫弗-拉普拉斯定理,

参数估计
点估计
- 矩估计

- 正态母体中用子样中位数和子样极差估计参数比较好计算。比如子样中位数近似服从 $N(\mu, \frac{\pi}{2n})$
- 最大似然估计

评定估计量好坏的标准
- 无偏性
- 相合性:对估计量的基本要求
- 有效性
- 优效估计
- 满足正规条件的无偏估计量的方差满足罗-克拉美不等式$$D\hat\theta \ge \frac{1}{nE(\frac{\partial{\ln f(x; \theta)}}{\partial{\theta}})^2} $$ 如果是离散母体,把 f 改为 P。
- 上面不等式右边称罗-克拉美下界,能达到且无偏的估计量就称优效估计;$n \rightarrow \infty$ 时能达到就是渐近优效估计
- 优效估计必是最小方差无偏估计量
- 优效估计
区间估计
- 置信区间:随机区间覆盖估计量的可能性 $P\{u_1 < U < u_2\} = 1 - \alpha$,$u_1$、$u_2$ 分别为上、下侧分位数。
- “弃真”的错误为第一类错误,“取伪”的错误为第二类错误。样本量一定时无法同时减小两类错误,显著性检验只对第一类错误的概率加以控制。
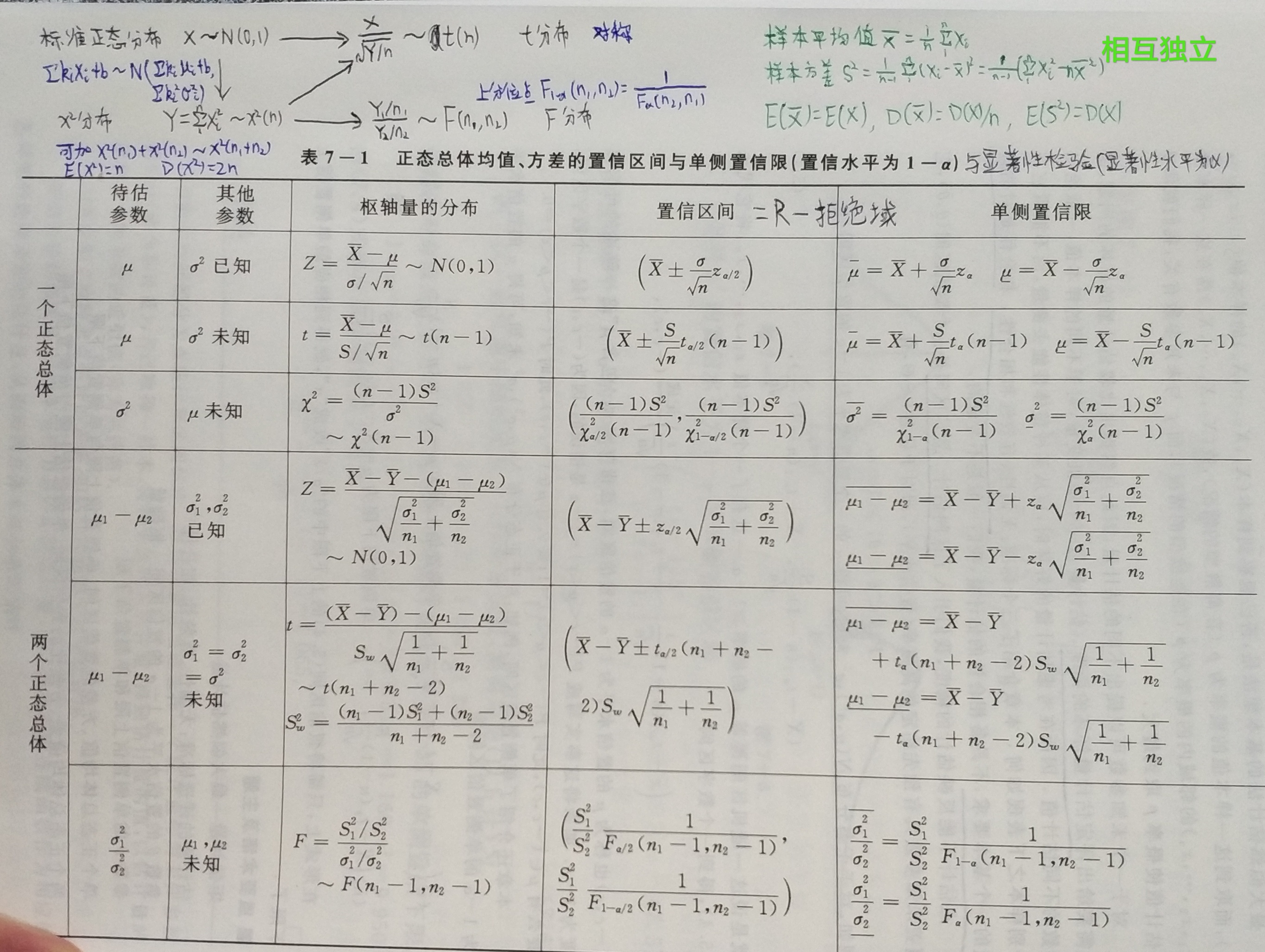
上图枢轴量的分布易由以下三点推出来:
- $\bar X \sim N(\mu, \sigma^2 / n)$
- $\frac{(n-1)S^2}{\sigma^2} \sim x^2(n-1)$
- $\bar X$ 与 $S^2$ 相互独立
大子样(比如超过 50)时可以有一些近似估计:
- 用子样的方差近似母体的方差
- 由中心极限定理,母体均值近似服从正态分布
- 由中心极限定理,n 很大时 $x^2(n)$ 近似于 N(n, 2n),所以 n > 45 时 $x^2$ 表里查不到上侧分位数,可以去查标准正态分布的表,然后乘以 $\sqrt{2n}$ 再加 n。
- t 分布是对称的,且随 n 增大趋近于标准正态分布,所以也可以查标准正态分布的表确定上侧分位数。
图中所示为常用的置信水平 95% 时两侧分位数:$z_{\alpha / 2} \approx 1.96$
假设检验
参数假设检验
- 在母体上做关于参数的原假设 $H_0$,例如均值大于某值、两个母体的方差之比等于 1(对立的假设称备择假设 $H_1$);
- 找统计量,在原假设成立的前提下导出该统计量的概率分布,如 $N, x^2, t, F$;
- 根据给定的显著性水平 $\alpha$ 与直观意义划分出拒绝域(按原假设这应是小概率事件)和接受域(单侧或两侧,对应区间估计中的置信区间);
- 根据子样的统计量的值落入的区域,接受或拒绝原假设;
- 如果拒绝假设,可以再对参数做区间估计。
p-value:当原假设为真时,比所得到的样本观察结果更极端的结果出现的概率。
分布假设检验:$x^2$ 检验法
假设 $H_0$:服从形式已知但参数未知的分布 $F(x) = F_0(x; \theta), \theta = (\theta_1, \theta_2, \cdots, \theta_k)$
- 抽取大子样($n \ge 50$)后通过极大似然估计出 $\hat\theta$
- 顺序取 l + 1 个点 $\alpha_0 < \alpha_1 < \cdots < \alpha_l$ 把子样分成 l 个组,区间 $(\alpha_{i-1}, \alpha_i]$ 中的理论频数如下(实际分组时各组理论频数不少于 5):$$np_i = n(F_0(\alpha_i, \hat\theta) - F_0(\alpha_{i-1}, \hat\theta))$$
- 实际频数 $m_i$
则频数的实际与理论的偏差渐近服从卡方分布 $$x^2 = \sum\limits_{i=1}^{l} \frac{(m_i - n p_i)^2}{np_i} \sim x^2(l - k - 1)$$ 又因为偏差越小越应该接受 $H_0$,因此可以按 $P\{x^2 \ge x_\alpha^2(l - k - 1)\} \approx \alpha$ 查上侧分位数拒绝假设,反之接受假设。
l 与 n 的关系有如下经验:
| n | l |
|---|---|
| 50 ~ 100 | 6 ~ 8 |
| 100 ~ 200 | 9 ~ 12 |
| 200+ | 15 ~ 20 |
假设 $H_0$:服从已知的 l 项的离散分布 $P(A_i) = p_i, i = 1, 2, \cdots, l$
也就是 k = 0 的情形
做 n 次(至少 50 次)独立重复试验,$m_i$ 是 $A_i$ 的频数。
按 $P\{x^2 \ge x_\alpha^2(l - 1)\} \approx \alpha$ 拒绝假设。
假设 $H_0: P(x, y) = P_1(x) P_2(y)$ (独立性假设检验)
有 n 组观测值 $(x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)$
将二维平面分为 r 行 s 列,设 $m_{ij}, m_i, m_j$ 分别为第 i 列第 j 行的矩形范围内的频数、第 i 列的频数和第 j 行的频数,并记 $n_{ij} = \frac{n_{i*}n_{*j}}{n}$,则在原假设成立时有 $$x^2 = \sum\limits_{i=1}^{s} \sum\limits_{k=1}^{r} \frac{(m_{ij} - n_{ij})^2}{n_{ij}} \sim x^2((r-1)(s-1))$$
方差分析:离差分析法
分解定理:设
- $X_1, X_2, \cdots, X_n$ 相互独立且 $X_i \sim N(0, 1)$
- $\sum\limits_{i=1}^{n} X_i^2 = \sum\limits_{i=1}^{k} Q_i$,$Q_i$ 是 $X_1, X_2, \cdots, X_n$ 的非负定二次型(线性组合的平方和)且自由度为 $f_i$
则 $\sum\limits_{i=1}^{k} f_i = n$ 等价于 $Q_1, Q_2, \cdots, Q_k$ 相互独立且 $Q_i \sim x^2(f_i)$
一元方差分析
因子 A 有 r 种水平:$A_1, A_2, \cdots, A_r$,在水平 $A_i$ 时实验结果服从正态分布:$X_i \sim N(\mu_i, \sigma^2)$(假定不同水平的方差都相等)。现在想知道该因子的不同水平是否对实验结果有显著影响(而不通过两两做检验进行比较)。
每种水平分别实验,$A_i$ 对应子样 {$X_{ij}, j = 1, 2, \cdots, n_i$}。设
- 组内均值 $\bar X_i = \frac1{n_i} \sum\limits_{j=1}^{n_i} X_{ij}$
- 总均值 $\bar X = \frac{\sum\limits_{i=1}^{r} \sum\limits_{j=1}^{n_i} X_{ij}}{\sum\limits_{i=1}^{r} n_i}$
| 单一因子 | 离差平方和 | 均方离差 | 原假设 | 假设成立时的分布 | 检验分布 |
|---|---|---|---|---|---|
| 组间 | $Q_A = \sum\limits_{i=1}^{r} n_i (\bar X_i - \bar X)^2$ | $S_A = \frac{Q_A}{r-1} $ | 无显著影响 $\mu_1=\mu_2=\cdots=\mu_r$ |
$\frac{Q_A}{\sigma^2} \sim x^2(r - 1)$ | $F_A = \frac{S_A}{S_E} \sim F(r - 1, n - r)$ |
| 组内 | $Q_E = \sum\limits_{i=1}^{r} \sum\limits_{j=1}^{n_i} (X_{ij} - \bar X_i)^2$ | $S_E=\frac{Q_E}{n-r}$ | - | $\frac{Q_E}{\sigma^2} \sim x^2(n - r)$ | - |
- $S_A \ge S_E$,等号成立当且仅当假设成立
- 直观上都是根据显著性水平取 F 分布的右侧分位数划分接受域与拒绝域(组间均方离差越大说明影响越显著)
- 如果原假设被拒绝,可以根据 $\frac{\bar X_i - \bar X_j - (\mu_i - \mu_j)}{\sqrt{\frac1{n_i} + \frac1{n_j}} \frac{Q_E}{n - r}} \sim t(n - r)$ 对两个水平之间的差异 $\mu_i - \mu_j$ 做区间估计。
二元方差分析
因子 A、B 分别有 r、s 种水平,在每组 $(A_i, B_j) \in A \times B$ 上各做 c 次实验,母体 $X_{ij}$ 服从方差为 $\sigma^2$ 的正态分布。子样为 {$X_{ijk}, k = 1, 2, \cdots, c$}。设
- 组内均值 $\bar X_{ij} = \frac1c \sum\limits_{k=1}^{c} X_{ijk}$
- 边缘均值(A)$\bar X_{i*} = \frac1s \sum\limits_{j=1}^{s} \bar X_{ij}$
- 边缘均值(B)$\bar X_{*j} = \frac1r \sum\limits_{i=1}^{r} \bar X_{ij}$
- 总均值 $\bar X = \frac1{sr} \sum\limits_{i=1}^{r} \sum\limits_{j=1}^{s} \bar X_{ij}$
| 两个因子 | 离差平方和 | 均方离差 | 原假设 | 假设成立时的分布 | 检验分布(c > 1) | 检验分布(c = 1) |
|---|---|---|---|---|---|---|
| 因子 A | $Q_A = sc \sum\limits_{i=1}^{r} (\bar X_{i*} - \bar X)^2$ | $S_A=\frac{Q_A}{r-1}$ | 因子 A 无显著影响 | $\frac{Q_A}{\sigma^2} \sim x^2(r-1)$ | $F_A = \frac{S_A}{S_E} \sim F(r - 1, rs(c - 1))$ | $F_A = \frac{S_A}{S_I} \sim F(r - 1, (r - 1)(s - 1))$ |
| 因子 B | $Q_B = rc \sum\limits_{j=1}^{s} (\bar X_{*j} - \bar X)^2$ | $S_B=\frac{Q_B}{s-1}$ | 因子 B 无显著影响 | $\frac{Q_B}{\sigma^2} \sim x^2(s-1)$ | $F_B = \frac{S_B}{S_E} \sim F(s - 1, rs(c - 1))$ | $F_B = \frac{S_B}{S_I} \sim F(s - 1, (r - 1)(s - 1))$ |
| 交互作用 | $Q_I = c \sum\limits_{i=1}^{r} \sum\limits_{j=1}^{s} (\bar X_{ij} - \bar X_{i*} - \bar X_{*j} + \bar X)^2$ | $S_I=\frac{Q_I}{(r-1)(s-1)}$ | 因子 A、B 无显著的交互作用 | $\frac{Q_I}{\sigma^2} \sim x^2((r-1)(s-1))$ | $F_I = \frac{S_I}{S_E} \sim F((r - 1)(s - 1), rs(c - 1))$ | - |
| 误差 | $Q_E = \sum\limits_{i=1}^{r} \sum\limits_{j=1}^{s} \sum\limits_{k=1}^{c} (X_{ijk} - \bar X_{ij})^2$ | $S_E=\frac{Q_E}{rs(c-1)}$ | - | $\frac{Q_E}{\sigma^2} \sim x^2(rs(c-1))$ | - | - |
- $\{S_A, S_B\} \ge S_I \ge S_E$,等号成立当且仅当对应的假设成立
- 直观上都是根据显著性水平取 F 分布的右侧分位数划分接受域与拒绝域(越大说明检验的因素影响越显著)
多个因子:正交试验设计
按照 $L_n(s^r)$ 正交表安排 n 次试验,希望能替代 $s^r$ 次试验检验 r 个(或略少于 r 个)各有 s 种水平的因子是否对试验结果有显著影响。
例如如下是 $L_9(3^4)$ 表,通过 9 次实验检验 4 个各有 3 种水平的因子的影响是否显著:
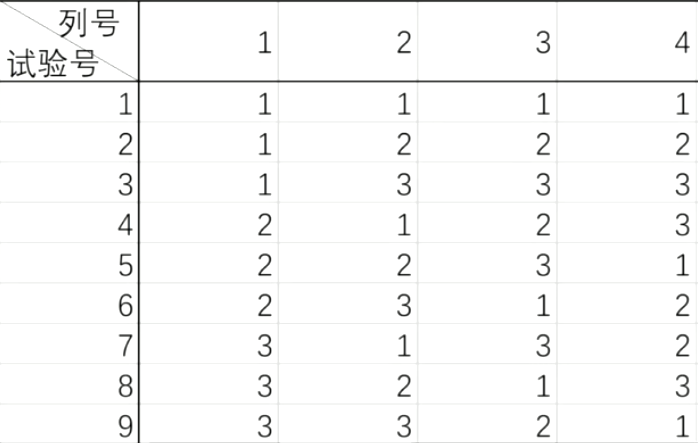
正交表的安排满足:
- 任一列各水平出现的个数相同
- 任意两列各组合水平出现的个数相同
按照正交表进行试验后,仅用已有结果求平均近似得到总均值与各个因子的边缘均值,进一步得
- 因子的离差平方和:(n / s) * 该因子各个水平时的 (边缘均值 - 总均值) 的平方和,自由度为 s - 1
- 总离差:各次试验 (结果 - 总均值) 的平方和,自由度为 n - 1
- 误差:总离差减去各个因子的离差平方和,自由度为 (n - 1) - r * (s - 1)
于是由 1 式 / 3 式应服从 F(r - 1, (n - 1) - r * (s - 1)) 去检验相应因子对试验结果是否有显著影响。
如果要考虑因子间两丙交互作用,就按照正交表附带的交互作用表,将因子对附加或新增到试验表的某些列上,计算与检验过程不变。
线性回归模型:$y = \alpha + \vec\beta \cdot \vec x + \epsilon$
其中 $\epsilon \sim N(0, \sigma^2)$,$\alpha, \vec\beta = (\beta_1, \beta_2, \cdots, \beta_p), \sigma^2$ 是待估计的参数。
参数的点估计
最小化 $$Q=\sum\limits_{i=1}^{n} (y - \alpha - \vec\beta \cdot \vec x)^2 = \| Y - \begin{pmatrix} 1 & X \end{pmatrix} \begin{pmatrix} \alpha \\ \vec\beta \end{pmatrix} \|^2 = \| Y - \tilde{X} \tilde \beta \|^2$$
令 Q 对 $\tilde \beta$ 各分量的偏导为 0 得最小二乘估计 $$\begin{cases} \hat\beta &= (\tilde{X}^T \tilde{X})^{-1} \tilde{X}^T Y \\ \hat\sigma^2 &= \frac1{n - p - 1} \sum\limits_{i=1}^{n} \hat\epsilon_i^2 \end{cases}$$ 且有相互独立的 $$\begin{cases} \hat\beta & \sim N(\tilde \beta, \sigma^2 (\tilde{X}^T \tilde{X})^{-1}) \\ \frac1{\sigma^2}\sum\limits_{i=1}^{n} \hat\epsilon_i^2 & \sim x^2(n - p - 1) \end{cases}$$
模型的检验
设 $\bar Y$为所有 y 的试验值的均值。用离差分析法,假设 $H_0: \vec\beta = 0 $ 成立,则有 $$F = \frac{n - p - 1}{p} \cdot (\frac{\sum\limits_{i=1}^{n}(Y_i - \bar Y)^2}{\sum\limits_{i=1}^{n} \hat\epsilon_i^2} - 1) \sim F(p, n - p - 1)$$ F 值大于分位数时则拒绝假设,认为线性回归显著。
系数的检验
$\hat\beta$ 的第 i 个分量可由 $$ T_i = \frac{\hat\beta_i - \tilde\beta_i}{\sqrt{\frac{c_{ii}}{n - p - 1} \sum\limits_{i=1}^{n} \hat\epsilon_i^2}} \sim t(n - p - 1)$$ 单独检验是否显著地等于 $\tilde\beta_i$,其中 $c_{ij}$ 是协方差矩阵 $C = (\tilde X^T \tilde X)^{-1}$ 中元素。特别地
- 取 $\tilde\beta_i = 0$ 可以检验相应的自变量分量是否重要;
- 取 $\tilde\beta_i = 0$ 且 p = 1 时也可以用这个分布检验线性回归是否显著。
因变量的区间估计
对任一点 $\vec x$ 做估计 $\hat y = \hat\beta \cdot (1, \vec x)$ 有 $$T = \frac{y - \hat y}{\sqrt{\frac{d}{n - p - 1} \sum\limits_{i=1}^{n} \hat\epsilon_i^2}} \sim t(n - p - 1)$$ 其中 $$d = 1 + \frac1n + \sum\limits_{i=1}^{p} \sum\limits_{i=1}^{p} c_{ij} (x_i - \bar x_i)(x_j - \bar x_j) = 1 + \frac1n + (x - \bar x)^T C (x - \bar x)$$ 可导出该估计的置信区间
古典假定的违背
| 违背方式 | 多重共线性 (1, x, u) 线性相关 |
异方差 $\sigma = \sigma(x)$ |
自相关 Cov $\epsilon$ 非对角 |
|---|---|---|---|
| 后果 | $c_{ii}$ 过大: * t 检验被接受 * 预测区间趋于无穷 |
$c_{ii}$ 不精确: * t 检验不精确 * 预测失效 |
$D\hat\beta$ 被低估: * t 检验不精确 * 预测失效 |
| 检验法 | 1. 部分 $x_i, x_j$ 的相关系数的绝对值接近 2. 增加或删除一个解释变量导致回归系数的估计发生较大变化 3. 重要解释变量的系数没有通过 t 检验 4. 回归系数的符号与理论相反 |
1. 图示法:绘出 $\hat\epsilon_i^2$ 与 $x_i$ 的图形 2. Goldfeld-Quanad 法:将 $Y_i$ 从小到大排列,删除中间 1/4 数据,对两边各 k 个数据分别回归,残差平方和的商应服从 F(k - p - 1, k - p - 1) 3. white 检验:将残差平方和与 x 做 2 次多项式回归(可化为线性回归),通过回归的显著性进行判断 |
DW 检验法:DW = $\frac{\sum (e_i - e_{i-1})^2}{\sum e_i^2} \approx 2(1 - \hat\rho)$ 即 $\hat\rho \approx 1 - DW / 2$ |
| 补救法 | 1. 增加样本容量 2. 剔除相关系数大的变量 3. 变换模型形式(如将模型差分) 4. 利用先验信息合并变量 5. 使用面板数据 (时间序列数据与截面数据结合) 6. 数据处理 7. 逐步回归法 |
1. 模型变换法:假设 $D \epsilon_i = f(x) \sigma^2$,f(x) 是二次式,则模型两边同除以 f(x) 消去异方差(配合 white 检验法) 2. 加权最小二乘法:设 Cov $\epsilon$ = A $\sigma^2$,因 A 对称得正交矩阵 Q 使 A 与单位矩阵合同,模型两边同时乘以 Q 可消去异方差 3. 对数变换法:用 (ln x, ln y) 替代 (x, y) |
1. 加权最小二乘法 2. 广义差分法:设 $\epsilon_t = \rho \epsilon_{t-1} + v_t$,其中 v 满足古典假定,于是模型换成 $y' = Y_t - \rho Y_{t-1}$ 可消去自相关 |
Page Not Found
Try to search through the entire repo.